Formula, lai aprēķinātu rentes maksājumu
Termins “mūža rente” attiecas uz periodisko maksājumu sērijām, kas jāsaņem vai nu katra perioda sākumā, vai arī perioda beigās nākotnē. Forma mūža rentes maksājumam un maksājamajai rentei tiek aprēķināta, pamatojoties uz mūža rentes PV, faktisko procentu likmi un vairāku periodu PV.
Formula, kuras pamatā ir parasta mūža rente, tiek aprēķināta, pamatojoties uz parastās rentes PV, faktisko procentu likmi un vairākiem periodiem.
Annuity = r * PVA parasts / (1 - (1 + r) -n )kur,
- PVA Parastais = parastās rentes pašreizējā vērtība
- r = faktiskā procentu likme
- n = Periodu skaits
Matemātiski mūža rentes vienādojums tiek attēlots kā
Anuitāte = r * PVA pienākas / ((1 - (1 + r) -n ) * (1 + r))kur,
- PVA Ņemot = pašreizējā vērtība annuitātes dēļ
- r = faktiskā procentu likme
- n = periodu skaits

Kā aprēķināt anuitātes maksājumu? (Soli pa solim)
Anuitātes maksājuma aprēķinu var iegūt, izmantojot parastās rentes PV šādās darbībās:
- 1. solis : Pirmkārt, nosakiet mūža rentes PV un apstipriniet, ka maksājums tiks veikts katra perioda beigās. To apzīmē ar PVA Ordinary .
- 2. solis: Pēc tam nosakiet procentu likmi, pamatojoties uz pašreizējo tirgus atdevi. Tad faktisko procentu likmi aprēķina, dalot gada procentu likmi ar periodisko maksājumu skaitu gadā, un to apzīmē ar r. r = gada procentu likme / regulāro maksājumu skaits gadā
- 3. solis: Pēc tam nosakiet periodu skaitu, reizinot periodisko maksājumu skaitu gadā un gadu skaitu, un tas tiek apzīmēts ar n. n = regulāro maksājumu skaits gadā * Gadu skaits
- 4. solis: Visbeidzot, mūža rentes maksājums, kas balstīts uz parastās rentes PV, tiek aprēķināts, pamatojoties uz parastās rentes PV (1. solis), faktisko procentu likmi (2. solis) un dažiem periodiem (3. solis), kā parādīts iepriekš.
Anuitātes maksājuma aprēķinu var arī iegūt, izmantojot maksājamās rentes PV šādās darbībās:
- 1. solis: Pirmkārt, nosakiet mūža rentes PV un apstipriniet, ka maksājums tiks veikts katra perioda sākumā. To apzīmē ar PVA Due .
- 2. solis: Pēc tam nosakiet procentu likmi, pamatojoties uz pašreizējo tirgus atdevi. Tad faktisko procentu likmi aprēķina, dalot gada procentu likmi ar periodisko maksājumu skaitu gadā, un to apzīmē ar r. r = gada procentu likme / regulāro maksājumu skaits gadā
- 3. solis: Pēc tam nosakiet periodu skaitu, reizinot periodisko maksājumu skaitu gadā un gadu skaitu, un tas tiek apzīmēts ar n. n = regulāro maksājumu skaits gadā * Gadu skaits
- 4. solis: Visbeidzot, mūža rentes maksājums, kas balstīts uz maksājamās rentes PV, tiek aprēķināts, pamatojoties uz maksājamās rentes PV (1. solis), faktisko procentu likmi (2. solis) un vairākiem periodiem (3. solis), kā parādīts iepriekš.
Piemēri
1. piemērs
Ņemsim piemēru no Dāvida, kurš laimēja loteriju 10 000 000 USD vērtībā. Viņš ir izvēlējies rentes maksājumu katra gada beigās nākamajiem 20 gadiem kā izmaksu iespēju. Nosakiet summu, kas Deividam tiks izmaksāta kā mūža rentes maksājums, ja nemainīgā procentu likme tirgū ir 5%.
Zemāk sniegti dati, kas izmantoti, lai aprēķinātu mūža rentes maksājumus.
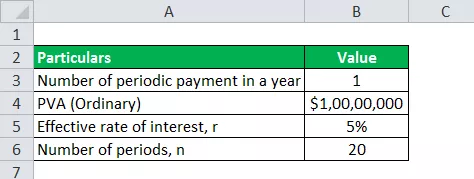
PVA parastais = 10 000 000 USD (kopš ikgadējā mūža rente jāmaksā katra gada beigās)
Tādēļ mūža rentes aprēķinu var veikt šādi:
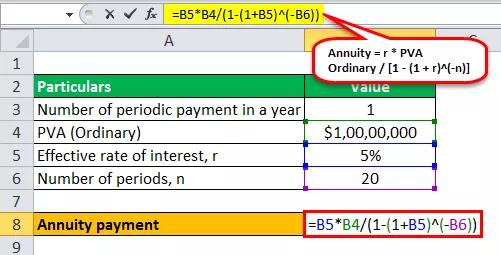
- Anuitāte = 5% * 10 000 000 USD / (1 - (1 + 5%) -20 )
Annuitātes maksājuma aprēķins būs -

- Annuitāte = 802 425,87 USD ~ 802 426 USD
Tāpēc parasto rentes gadījumā Dāvids maksās mūža rentes maksājumus nākamajos 20 gados 802 426 ASV dolāru apmērā.
2. piemērs
Ņemsim iepriekš minēto Dāvida piemēru un noteiksim mūža rentes maksājumu, ja tas tiek izmaksāts katra gada sākumā, ar visiem pārējiem nosacījumiem vienādus.
Annuitātes maksājumu aprēķināšanai mēs izmantosim tos pašus datus kā iepriekš minēto piemēru.
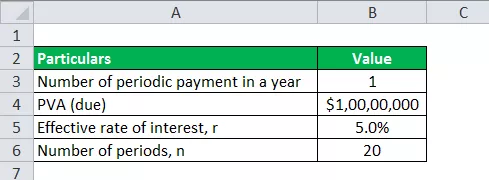
Tādēļ mūža rentes aprēķinu var veikt šādi:
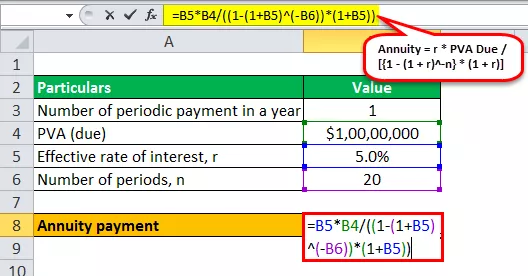
- Anuitāte = r * PVA pienākas / ((1 - (1 + r) -n ) * (1 + r))
- Anuitāte = 5% * 10 000 000 USD / ((1 - (1 + 5%) -20 ) * (1 + 5%))
Annuitātes maksājuma aprēķins būs -
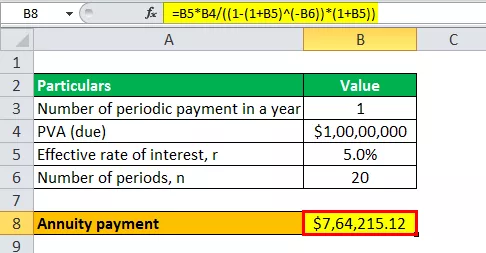
- Annuitāte = 764 215,12 USD ~ 764 215 USD
Tāpēc nākamajos 20 gados Dāvids maksās mūža rentes maksājumus USD 764 215 gadījumā, ja maksājama mūža rente.
Annuitu kalkulators
Varat izmantot šo Annuity Calculator.
| PVA Parasts | |
| r | |
| n | |
| Annuitas formula = | |
| Annuitas formula = | r * |
|
||||||||
| 0 * |
|
Atbilstība un lietojumi
Anuitātes maksājums ir viens no naudas laika vērtības pielietojumiem, ko papildus norāda starpība starp mūža rentes maksājumiem, kuru pamatā ir parasta mūža rente, un mūža rente, kas jāmaksā. Zemāks mūža rentes maksājums ir tāds, ka nauda tiek saņemta katra perioda sākumā. Tiek uzskatīts, ka līdzekļi tiks ieguldīti tirgū, un šajā periodā tiks nopelnīti procenti.
Gada rentes maksājuma vienādojumu var izmantot ienākumu rentes, amortizēto aizdevumu, loterijas izmaksu, strukturēto norēķinu un jebkura cita veida fiksētu periodisku maksājumu aprēķināšanā.








