Vidējais un svērtais vidējais ir divi dažādi termini excel, vidējais ir metode, lai aprēķinātu konkrētās datu kopas centrālo punktu, un to aprēķina kā tradicionālo vidējā aprēķināšanas veidu, saskaitot skaitļus, dalot ar esošo datu kopu, bet svērto vidējo ir vidējais rādītājs, kuru aprēķina tādā pašā veidā, bet ar svaru, kas reizināts ar katru datu kopu.
Starpība starp vidējo un svērto vidējo
Vidējais un vidējais svērtais ir matemātikas un statistikas termins finansēs un biznesā, taču abus aprēķina atšķirīgi. Vidējais rādītājs ir visu atsevišķo novērojumu summa, kas dalīta ar novērojumu skaitu. Vidējais, ko izmanto, lai atrastu vidējo vērtību konkrētā datu kopā. To sauc arī par centrālo tendenci, un to izmanto, lai atrastu datu grupas centrālo tendenci noteiktā datu grupā. Vidējo svērto vērtību izmanto grāmatvedības jomā. Un tā galvenais mērķis ir atrast pareizo svaru vai vērtību, kas jāatrisina. Vidējā svērtā vērtība ir noteiktu obligāciju vai aizdevumu pamatsummas atmaksa līdz pamatsummas samaksai.
Kas ir vidējais?
Vidējais rādītājs ir visu atsevišķo novērojumu summa, kas dalīta ar novērojumu skaitu. To izmanto, lai atrastu vidējo vērtību konkrētā datu kopā. To sauc arī par centrālo tendenci, un to izmanto, lai atrastu datu grupas centrālo tendenci noteiktā datu grupā. To galvenokārt izmanto datu attēlošanai. To var atrisināt datu kopai, izmantojot aritmētisko formulu.
Vidējā formula = novērojumu summa / novērojumu skaits
Vidējā piemērs
Apskatīsim piemēru, lai saprastu vidējo.
Pieņemsim, ka klasē ir desmit studenti ar atzīmēm 50, 60, 70, 80, 65, 78, 95, 63, 58, 91 no attiecīgi 100. Tagad ļaujiet mums atrast vidējo augstāk minēto studentu atzīmi, kā mēs zinām.
Vidējā formula = novērojumu summa / novērojumu skaits
Novērojumu summa = 50 + 60 + 70 + 80 + 65 + 78 + 95 + 63 + 58 + 91
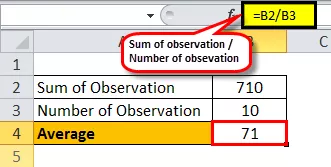
Tātad 10 skolēnu klases vidējais rādītājs ir 71.

Kāds ir vidējais svērtais rādītājs?
Vidējo svērto vērtību izmanto grāmatvedības jomā. Tās galvenais mērķis ir atrast pareizo svaru vai vērtību, kas jāatrisina. Vidējā svērtā vērtība ir noteiktu obligāciju vai aizdevumu pamatsummas atmaksa līdz pamatsummas samaksai. Svērtais vidējais ir arī vidējā līmeņa veids ar nelielu atšķirību, jo visiem novērojumiem nav vienāda svara; atšķirīgam novērojumam ir atšķirīga nozīme; katrs novērojums tiek reizināts ar svaru un summēts. Lai veiktu, tiek izmantots vidējais svars. To var uzskatīt par vidējo, kurā katrai vērtībai ir atšķirīgs svars. Un to ietekmē datu vērtības svars. Svērtā vērtība ir novērojuma produkta summa svarā, dalīta ar svara summu, un to var rakstīt kā:
Vidējā svērtā formula = (a1w1 + a2w2 + a3w3 +… + priekšlaicīga) / (w1 + w2 + w3… + wn)
Svērto vidējo piemērs
Apskatīsim piemēru, lai to labāk saprastu.
Pieņemsim, ka ir trīs dažādi eksāmeni, kas gada laikā dod pēdējās atzīmes. Katra eksāmena svars pirmajam eksāmenam bija 15%, otrajam eksāmenam - 25%, bet gala eksāmenam - 60%. Tagad pieņemsim, ka students pirmajā eksāmenā ir ieguvis 60 atzīmes, otrajā - 70 un 80 gala eksāmenā no 100, tagad aprēķināsim studenta gala atzīmes.
Lai to aprēķinātu, izmantojiet iepriekš minēto formulu.
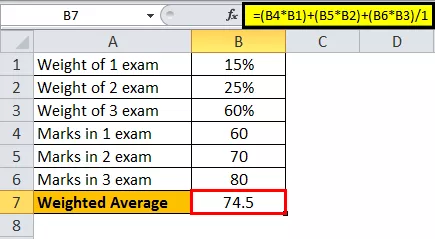
- Tātad studenta vidējā svērtā vērtība ir 74,5.
Vidēji pret vidējo svērto infografiku
Šeit mēs piedāvājam jums 5 galvenās atšķirības.

Vidējais un svērtais vidējais - galvenās atšķirības
Galvenās atšķirības starp šo vidējo ir šādas:
- Vidējais rādītājs ir visu atsevišķo novērojumu summa, kas dalīta ar novērojumu skaitu. Turpretī vidējo svērto vērtību novērošana reizina ar svaru un pievieno, lai atrastu risinājumu.
- Vidējais rādītājs ir matemātiskais vienādojums, turpretim svērto vidējo vērtību lieto finanšu ikdienas darbībās.
- Vidējais ir datu kopas attēlojums, bet vidējais svērtais ir jānovērtē, lai nonāktu pie problēmas risinājuma.
- Datu kopai vidējo var atrisināt, izmantojot aritmētisko formulu. Vidējam svērtajam komponentam tiek piešķirts vērtības svars, lai iegūtu konkrētu atbildi.
Vidējā un svērtā vidējā atšķirība starp galvu
Tagad aplūkosim atšķirības starp galvu.
| Pamats | Vidēji | Svērtais vidējais | ||
| Definīcija | Tā ir visu atsevišķo novērojumu summa, kas dalīta ar novērojumu skaitu. | Tas ir novērojums, kas reizināts ar svaru un saskaitīts, lai atrastu risinājumu. | ||
| Vienādojums | Tas ir matemātiskais vienādojums. | To piemēro ikdienas finanšu darbībās. | ||
| Risinājums | Tas ir datu kopas attēlojums. | Tai jānovērtē, lai nonāktu pie problēmas risinājuma. | ||
| Aprēķini | To var atrisināt datu kopai, izmantojot aritmētisko formulu. | Komponentam tiek piešķirts vērtības svars, lai iegūtu konkrētu atbildi. |
Secinājums
Tātad, mēs esam redzējuši vidējo un svērto vidējo un redzējuši atšķirību starp abiem. Mēs esam redzējuši, ka vidējais rādītājs ir visu individuālo novērojumu summa, kas dalīta ar novērojumu skaitu, un vidējo vērtību var atrisināt datu kopai, izmantojot aritmētisko formulu, savukārt svērtais vidējais ir novērojums, kas reizināts ar svaru un summēts, lai atrastu šķīdumam un vidējam svērtajam komponentam tiek piešķirts vērtības svars, lai iegūtu konkrētu atbildi. Abiem ir atšķirīgi lietotāji, pamatojoties uz problēmu, un abi tiek aprēķināti atšķirīgi. Vidējā svērtā vidējā mērķis ir atrast pareizo svaru vai vērtību, kas jāatrisina. Vidējā svērtā vērtība ir noteiktu obligāciju vai aizdevumu pamatsummas atmaksas vidējā vērtība līdz pamatsummas samaksai. Un vidējais tiek izmantots, lai atrastu vidējo vērtību vai vidējo vērtību.








