Kāds ir korelācijas koeficients?
Korelācijas koeficientu izmanto, lai noteiktu, cik stipra ir saistība starp diviem mainīgajiem, un tā vērtības var svārstīties no -1,0 līdz 1,0, kur -1,0 apzīmē negatīvu korelāciju un +1,0 ir pozitīva saistība. Tas ņem vērā relatīvās kustības mainīgajos un pēc tam nosaka, vai starp tiem ir kāda saistība.
Korelācijas koeficienta formula
r = n (∑xy) - ∑x ∑y / √ (n * (∑x 2 - (∑x) 2 )) * (n * (∑y 2 - (∑y) 2 ))
Kur
- r = korelācijas koeficients
- n = novērojumu skaits
- x = 1 st mainīgs kontekstā
- y = 2 nd mainīgs
Paskaidrojums
Ja pastāv kāda korelācija vai sakāms sakars starp diviem mainīgajiem, tad tas norāda, vai viens no mainīgajiem mainās vērtībā, tad arī otram mainīgajam būs tendence mainīties vērtībā, teiksim, konkrēti, kas varētu būt vai nu tajā pašā, vai pretējā virzienā. Vienādojuma skaitītāja daļa veic pārbaudi un relatīvo izturību mainīgajiem lielumiem, kas pārvietojas kopā, un vienādojuma saucēja daļa mērogo skaitītāju, reizinot mainīgo lielumu atšķirības no kvadrātiem.
Piemēri
1. piemērs
Apsveriet šādus divus mainīgos: x un y. Jums jāaprēķina korelācijas koeficients.
Zemāk ir sniegti dati aprēķinam.

Risinājums:
Izmantojot iepriekš minēto vienādojumu, mēs varam aprēķināt sekojošo

Mums ir visas iepriekšminētās tabulas vērtības ar n = 4.
Tagad ievadīsim vērtības korelācijas koeficienta aprēķināšanai.

Tāpēc aprēķins ir šāds,

r = (4 * 25 032,24) - (262,55 * 317,31) / √ ((4 * 20 855,74) - (262,55) 2 ) * ((4 * 30 058,55) - (317,31) 2 )
r = 16 820,21 / 16 831,57
Koeficients būs -

Koeficients = 0,99932640
2. piemērs
X valsts ir augošas ekonomikas valsts, un tā vēlas veikt neatkarīgu tās centrālās bankas lēmumu analīzi par procentu likmju izmaiņām, neatkarīgi no tā, vai tie ir ietekmējuši inflāciju un vai centrālā banka spēj to kontrolēt.
Pēc procentu likmes un inflācijas līmeņa, kas valstī valdīja vidēji šos gadus, kopsavilkuma ir sniegts zemāk.
Zemāk ir sniegti dati aprēķinam.

Valsts prezidents ir vērsies pie jums, lai nākamajā sanāksmē veiktu analīzi un sniegtu prezentāciju par to pašu. Izmantojiet korelāciju un nosakiet, vai centrālā banka ir sasniegusi savu mērķi.
Risinājums:
Izmantojot iepriekš apspriesto formulu, mēs varam aprēķināt korelācijas koeficientu. Procentu likmes traktēšana kā viens mainīgais, teiksim x, un inflācijas līmeņa traktēšana kā cits mainīgais kā y.

Mums ir visas iepriekšminētās tabulas vērtības ar n = 6.
Tagad ievadīsim vērtības korelācijas koeficienta aprēķināšanai.


r = (6 * 170,91) - (46,35 * 22,24) / √ ((6 * 361,19) - (46,35) 2 ) * ((6 * 82,74) - (22,24) 2 )
r = -5,36 / 5,88
Korelācija būs -

Korelācija = -0,92
Analīze. Šķiet, ka korelācija starp procentu likmi un inflācijas līmeni ir negatīva, kas, šķiet, ir pareiza saistība. Palielinoties procentu likmei, inflācija samazinās, kas nozīmē, ka tām ir tendence virzīties pretējā virzienā viena no otras, un no iepriekš minētā rezultāta izriet, ka centrālā banka veiksmīgi īstenoja lēmumu, kas saistīts ar procentu likmju politiku.
3. piemērs
ABC laboratorija veic pētījumus par augumu un vecumu, un vēlējās uzzināt, vai starp tiem pastāv kāda saistība. Viņi ir savākuši 1000 cilvēku izlasi katrai no kategorijām un ir izdomājuši vidējo augstumu šajā grupā.
Zemāk ir sniegti dati korelācijas koeficienta aprēķināšanai.

Jums jāaprēķina korelācijas koeficients un jānāk pie secinājuma, ka, ja pastāv kāda saistība.
Risinājums:
Apstrādājot vecumu kā vienu mainīgo, teiksim, x, un augstumu (cm

Mums ir visas iepriekšminētās tabulas vērtības ar n = 6.
Tagad ievadīsim vērtības korelācijas koeficienta aprēķināšanai.

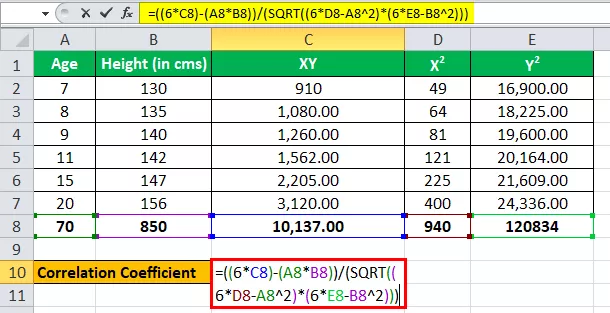
r = (6 * 10 137) - (70 * 850) / √ ((6 * 940 - (70) 2 ) * ((6 * 1,20,834) - (850) 2 )
r = 1 322,00 / 1 361,23
Korelācija būs -

Korelācija = 0,971177099
Atbilstība un izmantošana
To statistikā galvenokārt izmanto, lai analizētu attiecības starp aplūkojamajiem mainīgajiem lielumu, kā arī tālāk mēra, vai starp dotajiem datu kopumiem ir kāda lineāra sakarība un cik labi tie varētu būt saistīti. Viens no kopējiem korelācijā izmantotajiem pasākumiem ir Pīrsona korelācijas koeficients.
Ja mainīgais mainās vērtībā un kopā ar šo citu mainīgo mainās vērtība, tad šīs attiecības izpratne ir kritiska, jo var izmantot pirmā mainīgā vērtību, lai prognozētu otrā mainīgā vērtības izmaiņas. Šajā mūsdienu laikmetā korelācijai ir daudz dažādu lietojumu, piemēram, to izmanto finanšu nozarē, zinātniskos pētījumos un kur nē. Bet tomēr ir svarīgi zināt, ka korelācijai ir trīs galvenie attiecību veidi. Pirmais ir pozitīvas attiecības, kas norāda, ja mainās mainīgā vērtība, tad saistītā mainīgā mainīsies tajā pašā virzienā. Līdzīgi, ja pastāv negatīvas attiecības, tad saistītais mainīgais izturēsies pretēji. Turklāt, ja nav korelācijas, r nozīmē nulles vērtību.Skatiet zemāk redzamos attēlus, lai labāk izprastu jēdzienu.









