Kas ir diapazona formula?
Diapazona formula attiecas uz formulu, kuru izmanto, lai aprēķinātu starpību starp diapazona maksimālo vērtību un minimālo vērtību, un saskaņā ar formulu minimālā vērtība tiek atņemta no maksimālās vērtības, lai noteiktu diapazonu.
Diapazons = maksimālā vērtība - minimālā vērtība
No norādītās datu kopas, kas statistikas darbiniekiem un matemātiķim sniedz labāku izpratni par datu kopu, cik tā ir daudzveidīga. Tā ir vienkāršākā pieeja statistikas dispersijas aprēķināšanai.
Paskaidrojums
Tas ir diezgan vienkārši un ērti lietojams, jo formula norāda tā maksimālo vērtību, no kuras atņemta dotā parauga minimālā vērtība. Tāpēc dispersija starp maksimālo vērtību un minimālo vērtību ir diapazons, un, lai arī to ir viegli lietot un saprast, tas ir jāinterpretē pareizi.
Piemēram, ja datos ir kontūrzīmulis, diapazonu ietekmētu tas pats un rezultāts iegūtu nepareizu informāciju. Ņemiet praktisku piemēru norādītajiem datiem 2, 4, 7, 7, 100, tad diapazons būtu 100 - 2, kas ir 98, bet, kā redzams, datu diapazons ir zem 10, bet, ņemot vērā un interpretējot, ka dati ir 98 novedīs pie nepareizas informācijas sniegšanas. Tāpēc diapazona interpretācija jāveic, pienācīgi apsverot.
Piemēri
1. piemērs
Apsveriet iespēju sekot norādītajai datu kopai 2,2,4,4, 4, 6,7,7,8, 8, 8, 9, 9, 9, 9, 9. Jums jāaprēķina diapazons šim paraugam.
Risinājums:
- Maksimālā vērtība = 9
- Minimālā vērtība = 2
Diapazons = 9 - 2
Diapazons = 7
2. piemērs
Mr Stark, zinātnieks, kurš 10 gadus strādā uzņēmumā ar nosaukumu Dream moon. Arora kungs, viņa vadītājs, veic eksperimentu ar cilvēku veselību un ir savācis dažus parauga datus par vīriešu augumu, kas ir 162, 158, 189, 144, 151, 150, 151, 178, 155, 160. Tagad viņš ir apjukums un vēlas uzzināt, cik daudz datu ir dažādi. Pie Starka kunga, kurš ir pieredzējis statistikas eksperts, vērsās viņa vadītājs Arora kungs, lai novērstu neskaidrības par formulas variācijām. Arora kungam ir jāsniedz atbilde savam vadītājam; jums jāaprēķina, cik daudz dati mainās?
Risinājums:
Diapazons = maksimālā vērtība - minimālā vērtība
- Maksimālā vērtība = 189
- Minimālā vērtība = 144
Diapazons = 189 - 144
Diapazons = 45
Savākto datu vai parauga variācijas ir 45.
3. piemērs
Bufeta kungs, labi pazīstams un cienījams investors visā pasaulē, tagad apsver ASV tirgus akcijas un pašlaik analizē dažus no tiem, kur viņš vēlas ieguldīt. Sarakstā ir iekļautas lielākās zilo mikroshēmu kompānijas ASV. Zemāk ir doti izvēlētie akcijas vai vērtspapīri, kā arī to jaunākā akciju tirgus cena, kas apzīmēta ASV dolāros, kur viņš apsver iespēju ieguldīt.
Jums jāaprēķina diapazons un jānāk klajā ar variantu sarakstu.
Risinājums:
Zemāk ir sniegti dati diapazona aprēķināšanai.
Izmantojot iepriekš minēto informāciju, Excel maksimālā vērtība tiks aprēķināta šādi,

Maksimālā vērtība = 204,66
Min vērtības Excel aprēķināšana ir šāda,
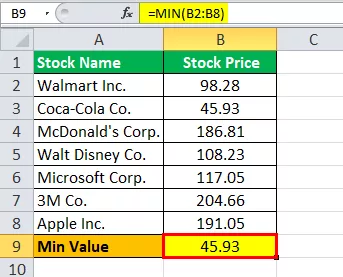
Min. Vērtība = 45,93
Tāpēc diapazona aprēķins ir šāds,

Diapazons = 204,66 - 45,93
Diapazons būs -
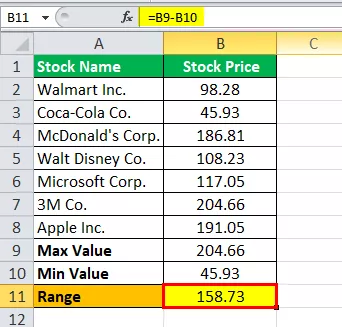
Diapazons = 158,73
Diapazona formulas izmantošana
Diapazons savā veidā ir ļoti viegli un ļoti vienkārši saprotams, kā sadalīti skaitļi dotajā datu kopā vai dotajā izlasē, jo, kā jau iepriekš minēts, aprēķinu veikt ir samērā viegli, jo ir nepieciešama tikai ļoti aritmētiskai operācijai, kas tikai atņem minimumu no maksimālās vērtības, bet diapazonā tam ir nedaudz vairāk lietojumu attiecībā uz noteiktu datu kopu vai noteiktu statistikas paraugu. Diapazons ir noderīgs arī, lai novērtētu citu izplatības mēru, ko sauc par dispersiju vai standartnovirzi.
Diapazons, kā minēts iepriekš, var sniegt informāciju tikai par pamatdetaļām, ti, kur atradīsies noteiktā parauga vai datu kopas izplatība. Piešķirot atšķirību vai sakot dispersiju starp noteiktā parauga vai attiecīgās datu kopas augstāko un zemāko vērtību, tas dod vienu informāciju vai aptuvenu priekšstatu par nozīmīgākajiem galējiem novērojumiem par to, cik plaši tie ir izplatīti, bet atkal tas nedod mājiens vai jebkura informācija par citiem datu punktiem, kur tie atrodas, kas ir galvenais diapazona vienādojuma izmantošanas vājums.
Diapazons, kā apspriests iepriekš, ir noderīgs, lai attēlotu izkliedi noteiktā paraugā vai noteiktā datu kopā, un tālāk to izmanto arī, lai salīdzinātu iegūto starpību starp to pašu norādīto paraugu vai to pašu norādīto datu kopu.








