Vienkāršs ietaupījumu kalkulators
Vienkāršo uzkrājumu kalkulatoru var izmantot, lai aprēķinātu termiņa summu, kas ir pieejama personai, kurā viņam ir iespējas ieguldīt, un viņš izvēlēsies, kur viņš var palielināt savu atdevi.
Vienkāršs ietaupījumu kalkulators
M = I * (1 + r) n * F + i * ((1 + r) n * F - 1) / r
Kurā,- Es esmu sākotnējā ieguldītā summa.
- r ir procentu likme.
- n ir periodu skaits, par kuriem jāveic vienkārši uzkrājumi.
- F ir procentu maksāšanas biežums
- i ir fiksētā summa, kas ieguldīta regulāri.
Par vienkāršo uzkrājumu kalkulatoru
Formula ir šāda:
Matemātiski to var aprēķināt vienreizējiem vienkāršajiem uzkrājumiem:
M = I * (1 + r / F) n * FOtrkārt, ja tiek veikti ikmēneša vienkārši uzkrājumi, aprēķins:
M = I * (1 + r) n * F + i * ((1 + r) n * F - 1 / r)Kurā,
- M ir kopējā summa vienkāršā uzkrājuma perioda beigās
- Es esmu sākotnējā ieguldītā summa
- i ir fiksētā summa, kas ieguldīta regulāri
- r ir procentu likme
- F ir procentu maksāšanas biežums
- n ir periodu skaits, par kuriem jāveic vienkārši uzkrājumi.
Ir daudz banku un citu finanšu iestāžu, kas konkurē tirgū, lai piesaistītu noguldījumus, lai viņi varētu veikt vairāk uzņēmējdarbības, ti, aizdot naudu korporācijām vai privātpersonām ar lielu neto vērtību. Dažas bankas maksātu lielāku procentu likmi, ja noguldījumi pārsniegtu noteiktus sliekšņa limitus un tiktu turēti kontā, pretējā gadījumā viņi maksās standarta procentu likmi. Turklāt procentu izmaksas varētu būt atšķirīgas; piemēram, procentus var palielināt un izmaksāt reizi ceturksnī, pusgadā vai gadā atkarībā no bankas. Tāpēc, izmantojot šo kalkulatoru, indivīdi varētu noteikt, kura finanšu iestāde viņiem izvēlas ieguldīt savu naudu, salīdzinot termiņa summu vai peļņu, kas nopelnīta par viņu pamatsummām.
Kā aprēķināt vienkāršos ietaupījumus?
Lai aprēķinātu vienkāršos ietaupījumus, ir jāveic šādas darbības.
1. solis - nosakiet, kāda summa būtu jāinvestē, neatkarīgi no tā, vai tā ir vienreizēja, vai ir arī periodisks ieguldījums, tad tas pats jāņem vērā, salīdzinot ietaupījumu likmju aprēķinus.
2. solis - noskaidrojiet procentu likmi, kas ir pieejama individuālajās opcijās un kura tiks nopelnīta vai ir sagaidāma nopelnīt no vienkāršajiem ietaupījumiem.
3. solis - Tagad nosakiet periodu, uz kuru tas tiks ieguldīts, un galvenokārt tas būs ilgtermiņa un būs atkarīgs no katra atsevišķa gadījuma.
4. solis - daliet procentu likmi ar procentu vai vienkāršo uzkrājumu procentu maksāšanas periodu skaitu. Piemēram, ja samaksātā likme ir 5% un tā maksā katru mēnesi, tad procentu likme būtu 5% / 12, kas ir 0,416%.
5. solis. Tagad izmantojiet formulu, kas tika apspriesta iepriekš 1. punktā), ja vienkāršie uzkrājumi tiek veidoti vienreizēji, un izmantojiet 2. formulu), ja vienkāršo uzkrājumu summa tiek veikta regulāri, kopā ar jebkuru sākotnējo summu visām pieejamajām opcijām .
6. solis - iegūtais skaitlis būs termiņa summa, kas ietvertu arī ienākumus no vienkāršajiem uzkrājumiem un izvēlētos to, kurai procentuāli ir vislielākā izmaksa.
Vienkārša ietaupījumu kalkulatora piemērs
Viljama kungs tagad ir pilngadīgs un ir priecīgs atvērt savu pirmo krājkontu. Viņš ir meklējis finanšu iestādi, kas nodrošina augstu procentu likmi, taču viņš ir neizpratnē, jo nesaņem to, kura banka viņam sniegs visaugstāko atdevi. Zemāk ir citāti, kurus Viljama kungs ir iekļāvis sarakstā.

Viņš vēlas ieguldīt 1500 USD jebkurā no kontiem, un viņš ieguldīs veidu, kā konts maksā procentus. Piemēram, ja banka maksā reizi gadā, tad summa tiks ieguldīta vienādi katra perioda beigās un turpinās to darīt 10 gadus.
Pamatojoties uz sniegto informāciju, jums jāaprēķina summa, ko viņš ietaupītu, un par to nopelnītie procenti un banka, kurā viņš izvēlētos ieguldīt.
Risinājums:
Mums tiek sniegta šāda informācija:
I BANKA
- I = Sākotnējā summa būs nulle
- r = procentu likme, kas ir 3,00%, un ceturksnī tā būs 3,00% / 4, kas ir 0,75%
- N = biežums, kas šeit ir reizi ceturksnī; līdz ar to būs 4
- n = veicamo vienkāršo uzkrājumu gadu skaits, kas šeit ir 10 gadi.
- i = Tā ir regulārā ieguldāmā summa, kas ir 1500/4, kas ir 375 USD

Tagad mēs varam izmantot tālāk norādīto formulu, lai aprēķinātu termiņa summu.
M = I * (1 + r) n * F + i * ((1 + r) n * F - 1) / r
- = 0 * (1 + 0,75%) 10 * 4 + 375 * ((1 + 0,75%) 10 * 4 - 1 / 0,75%)
- = 17,417,43
Termiņa summa būs 17 417,43
Nopelnītie saliktie procenti būtu USD 17 417,43 - USD (375 * 40) = 2417,43 USD.

BANKA II
- I = Sākotnējā summa būs nulle
- r = procentu likme, kas ir 3,12%, un pusgada laikā tā būs 3,12% / 2, kas ir 1,56%.
- N = biežums, kas šeit ir pusgads, tātad tas būs 2
- n = veicamo vienkāršo uzkrājumu gadu skaits, kas šeit ir 10 gadi.
- i = tā ir regulārā ieguldāmā summa, kas ir 1500/2, kas ir 750 USD

Tagad mēs varam izmantot tālāk norādīto formulu, lai aprēķinātu termiņa summu.
M = I * (1 + r) n * F + i * ((1 + r) n * F - 1 / r)
- = 0 * (1 + 1,56%) 10 * 2 + 750 * ((1 + 1,56%) 10 * 2 - 1) / 1,56%
- = 17 445,58 USD
Termiņa vērtība būs 17 445,58 USD
Nopelnītie saliktie procenti būtu 17 445,58 USD - (750 USD * 20) = 2445,58 USD.

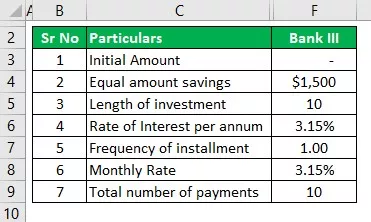
BANKA III
- I = Sākotnējā summa būs nulle
- r = procentu likme, kas ir 3,15%, un gadā tā būs 3,15% / 1, kas ir 3,15%
- N = Biežums, kas šeit ir katru gadu, tātad tas būs 1
- n = veicamo vienkāršo uzkrājumu gadu skaits, kas šeit ir 10 gadi.
- i = Tā ir regulārā ieguldāmā summa, kas ir 1500/1, kas ir 1500 USD
Tagad mēs varam izmantot tālāk norādīto formulu, lai aprēķinātu termiņa summu.
M = I * (1 + r) n * F + i * ((1 + r) n * F - 1) / r
- = 0 * (1 + 3,15%) 10 * 1 + 1500 * ((1 + 3,15%) 10 * 1 - 1) / 3,15%
- = 17 315,08 USD
Termiņa summa būs USD 17 315,08
Nopelnītie saliktie procenti būtu 17 315,08 USD - (1500 USD * 10) = 2315,08 USD.

Vislielākā nopelnītā summa ir II bankā, un tāpēc viņam vajadzētu atvērt kontu II bankā.

Secinājums
Šo kalkulatoru, kā jau tika apspriests iepriekš, var izmantot, lai salīdzinātu dažādas termiņa summas visā finanšu iestādē, jo augstāka procentu likme negarantē augstāko absolūto summu, kā redzams iepriekšējā piemērā. Tādējādi vajadzētu aprēķināt un salīdzināt summas visā termiņā un pēc tam pieņemt lēmumu.





